
Liczby kwantowe
Ruch elektronu wokół jądra atomowego można matematycznie opisać za pomocą równania Schrӧedingera. Jego rozwiązaniem jest funkcja falowa – orbital. Orbital to obszar wokół jądra atomowego, w którym prawdopodobieństwo znalezienia danego elektronu jest największe. Stan elektronu można opisać za pomocą liczb kwantowych. Wyróżnia się 5 liczb kwantowych: główną liczbę kwantową n, poboczną liczbę kwantową l, magnetyczną liczbę kwantową m, magnetyczną spinową liczbę kwantową ms i spinową liczbę kwantową s. Znajomość liczb kwantowych pozwala przewidzieć gdzie, z największym prawdopodobieństwem, znajdziemy dany elektron.
Główna liczba kwantowa n
- odnosi się do całkowitej energii elektronu,
- mówi o liczbie powłok i rozmiarach obszaru orbitalnego – im większa wartość n, tym elektron znajduję się średnio więcej czasu dalej od jądra atomowego,
- przyjmuje wartości kolejnych liczb całkowitych n = 1,2,3 itd., co odpowiada kolejno nazwom powłok K, L, M itd.
Maksymalną liczbę elektronów mogących znajdować się na danej powłoce określa wzór 2n2.
Wszystkie elektrony obsadzone na danej powłoce elektronowej mają tą samą wartość n.
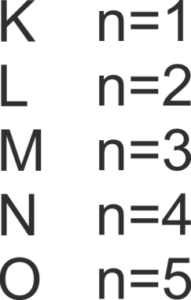
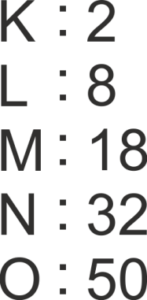
Poboczna liczba kwantowa (orbitalna) l
- decyduje o kształcie obszaru orbitalnego,
- przyjmuje wartości od l = 0 do l = n-1.
Jeśli dany elektron znajduje się na pierwszej podpowłoce danej powłoki wtedy poboczna liczba kwantowa przyjmuje wartość 0, a podpowłoka zbudowana jest z orbitalu typu s. Jeśli elektron znajduje się na drugiej podpowłoce danej powłoki wtedy wartość l opisująca ten elektron wynosi 1, a podpowłoka zbudowana jest z orbitali typu p. Jeśli elektron znajduje się na 3 podpowłoce danej powłoki wartość l opisująca ten elektron wynosi 2, a podpowłoka zbudowana jest z orbitali typu d.
Liczba podpowłok na danej powłoce uwarunkowana jest liczbą n tej powłoki i tak np.:
dla powłoki K -> n = 1 więc l przyjmuje jedynie wartość 0 (l = n-1 = 1-1 = 0),
dla powłoki L -> n = 2 więc l = 0,1 (podpowłoka 2s i 2p)
dla powłoki M -> n = 3 więc l = 0,1,2 (podpowłoka 3s, 3p, 3d),
dla powłoki N -> n = 4 więc l = 0,1,2,3 (podpowłoka 4s, 4p, 4d, 4f).
Wszystkie elektrony obsadzone na danej podpowłoce mają tą samą wartość n i l.
Magnetyczna liczba kwantowa m
- określa liczbę orbitali w danej podpowłoce,
- decyduje o orientacji przestrzennej obszaru orbitalnego w zewnętrznym polu magnetycznym
- przyjmuje wartości od –l do +l.
- Dla orbitalu typu s -> l = 0 więc m = 0 (możliwa jest jedna orientacja orbitalu typu s – stąd podpowłoka „składa się” z jednego orbital typu s – 1 klatka w schemacie graficznym),
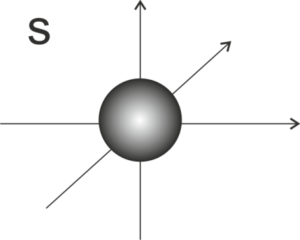
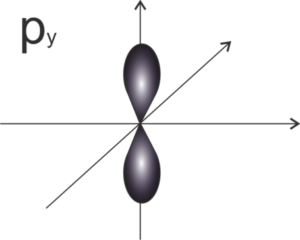
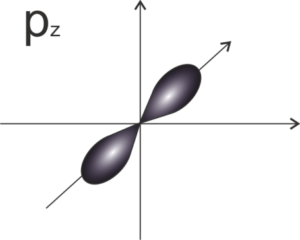
- dla orbitali typu p -> l = 1 więc m =-1, 0, 1 (możliwe są 3 orientacje w przestrzeni orbitalu p – stąd podpowłoka „składa się” z trzech orbitali typu p: px, py i pz – 3 klatki w schemacie graficznym):
| |
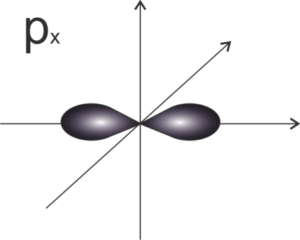
- dla orbitali typu d -> l = 2 więc m = -2,-1, 0, 1, 2 (możliwych jest 5 orientacji w przestrzeni orbitali d – stąd podpowłoka „składa się” z pięciu orbitali typu d – 5 klatek w schemacie graficznym),
| | | | | |
- dla orbitali typu f -> l = 3 więc m = -3, -2, -1, 0, 1, 2, 3 (możliwych jest 7 orientacji
w przestrzeni orbitali f – stąd podpowłoka „składa się” z siedmiu orbitali typu f – 7 klatek w schemacie graficznym).
| | | | |
Wszystkie elektrony „obsadzone” na danym orbitalu mają tą samą wartość n, l, m.
Magnetyczna spinowa liczba kwantowa ms
- określa spin elektronu (spin – kręcić się),
- przyjmuje wartości + ½ lub – ½
Na danym orbitalu elektrony różnią się od siebie wartością ms
Graficznie są to elektrony w tej samej klatce, różniące się zwrotem strzałki (spinem).
Spinowa liczba kwantowa s
- podaje wartość spinu, czyli wielkości fizycznej charakteryzującej właściwości magnetyczne elektronu,
- dla elektronu zawsze przyjmuje wartość ½.
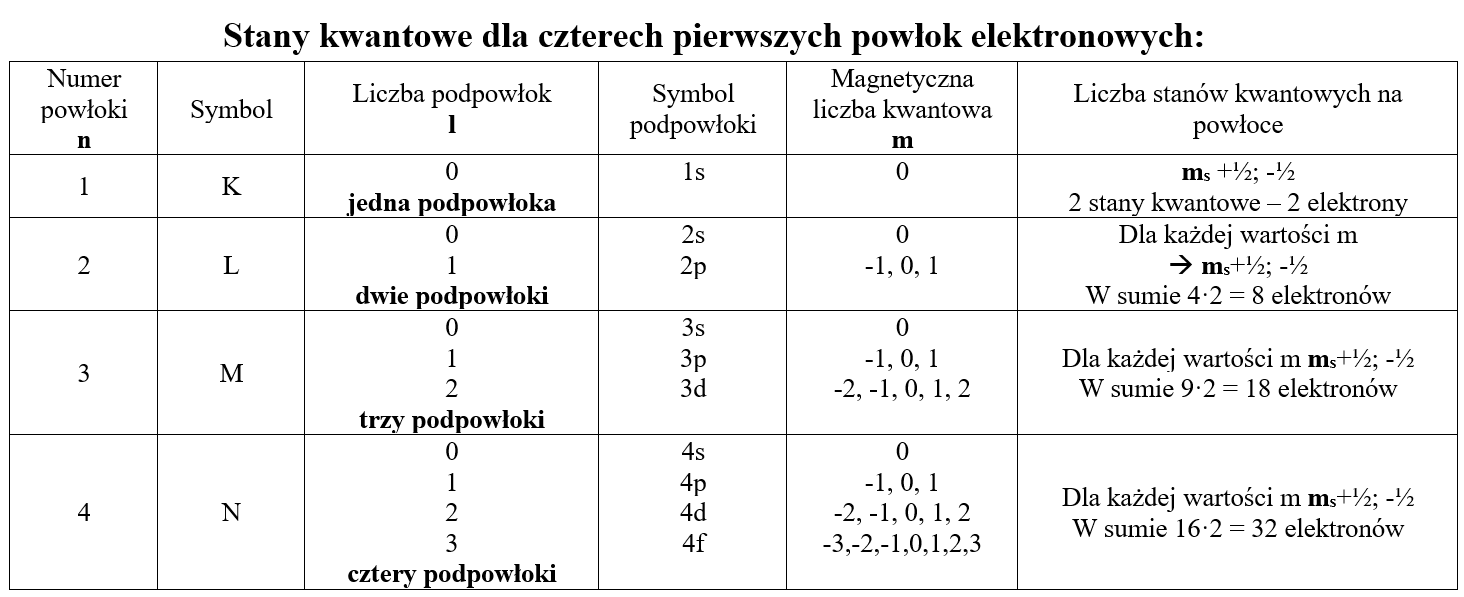
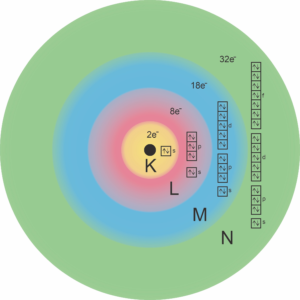
Stany kwantowe dla czterech pierwszych powłok elektronowych:
Ten artykuł może Cię zainteresować – Czym są powłoki, podpowłoki i orbitale w chemii?
Autorskie zadania w stylu maturalnym
Zadanie 1.
Uzupełnij poniższe zdania, tak aby zawierały poprawne informacje.
W stanie podstawowym atom arsenu posiada ……………………………… niesparowane elektrony, które należą do podpowłoki …………………………………………. Główna liczba kwantowa opisująca te elektrony przyjmuje wartość ………………………………………., a ………………………………………………………. jest równa 1.
Odpowiedź:
W stanie podstawowym atom arsenu posiada trzy niesparowane elektrony, które należą do podpowłoki 4p. Główna liczba kwantowa opisująca te elektrony przyjmuje wartość 4, a poboczna liczba kwantowa l jest równa 1.
Zadanie 2.
Dwa pierwiastki chemiczne oznaczone umownie literami A i B należą do tego samego okresu układu okresowego pierwiastków. Dodatkowo wiadomo, że w stanie podstawowym:
- atomy pierwiastków A i B mają na zewnętrznej powłoce po jednym elektronie niesparowanym.
- Stan energetyczny tych niesparowanych elektronów opisują główna liczba kwantowa n = 4 oraz poboczna liczba kwantowa l = 1.
- Masa atomowa pierwiastka B jest większa od masy atomowej pierwiastka A.
2.1.
Uzupełnij poniższą tabelę, wpisz symbole chemiczne pierwiastków A i B, numer grupy i symbol bloku konfiguracyjnego, do którego należy każdy z opisanych pierwiastków chemicznych.
| Symbol pierwiastka | Numer grupy | Numer bloku konfiguracyjnego | |
| Pierwiastek A | |||
| Pierwiastek B |
Odpowiedź:
| Symbol pierwiastka | Numer grupy | Numer bloku konfiguracyjnego | |
| Pierwiastek A | Ga | 13 | p |
| Pierwiastek B | Br | 19 | p |
2.2.
Napisz fragment konfiguracji elektronowej atomów A i B, w stanie podstawowym, opisujący rozmieszczenie elektronów walencyjnych na podpowłokach. Zastosuj graficzny zapis konfiguracji elektronowej, oraz uwzględnij numer powłoki i symbole podpowłok.
…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………..
Odpowiedź:
Ga:
| ↑↓ |
| ↑ | |
Br:
| ↑↓ |
| ↑↓ | ↑↓ | ↑↓ |
Zadanie 3.
Elektrony atomu pierwiastka X, w stanie podstawowym, zajmują 13 orbitali, przy czym 10 z nich jest całkowicie zapełnionych. Elektony walencyjne tego pierwiastka położone są na orbitalach różniących się zarówno główną liczbą kwantową n, jak i poboczną liczbą kwantową l.
Zidentyfikuj pierwiastek X oraz napisz fragment konfiguracji elektronowej atomu pierwiastka X, w stanie podstawowym, opisujący rozmieszczenie elektonów walencyjnych na podpowłokach. Zastosuj schemat klatkowy oraz uwzględnij numer powłoki i symbole podpowłok.
…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………..
Odpowiedź:
Szukanym pierwiastkiem X jest Vanad.
Ga:
| ↑↓ |
| ↑ | ↑ | ↑ | | |
Uwaga: Elektrony niesparowane muszą mieć zgodny spin.
Więcej o liczbach kwantowych dowiesz się w moim kursie, część 1.


